A novel algorithm for fast representation of a Pareto front with adaptive resolution: application to multi-objective optimization of a chemical reactor
効率的なパレート解の探索
前提:トレードオフについて
ベクトル $y^*$ がパレート最適であるとは,次を満たす $y \in S$ が存在しないことである:
\[\min_{u(\epsilon),x(\epsilon),p,\epsilon_f} \{J_1, J_2, \ldots, J_m\}\] \[J_i(y) \leq J_i(y^*) \quad \text{for all } i=1,2,...,m\]かつ
\[J_i(y) < J_i(y^*) \quad \text{for at least one } i\]すなわち,ある目的を改善しようとすると,他の目的が悪化するような状況である.このとき,$y^*$ は他のどの実行可能解よりも支配されていない(non-dominated).これは,目的が互いに競合していない限り,一意な解は存在しないことを意味する.このような非支配解の全体集合を パレートフロント(Pareto front) と呼ぶ
パレートフロントを求める方法
パレートフロントを得るための方法は大きく 2 つの分類に分けられる:ベクトル化法(vectorization methods) と スカラー化法(scalarization methods) である.
スカラー化手法
スカラー化手法の BAD POINT
- 複雑な制約条件への対応が困難であること
- 計算時間が長いこと
- 探索空間の次元数が高い場合に制限を受けること
スカラー化手法の GOOD POINT
- 多数の設計変数や制約条件を扱うことが可能である
重み付き和法(Weighted Sum method, WS)
\[\min_{y} \sum_{i=1}^{m} w_i J_i(y) = w^\top J(y)\]ただし w は以下を満たす.
\[w_i \geq 0 \quad (i = 1, 2, \ldots, m), \quad \sum_{i=1}^{m} w_i = 1\]つまり重みってこと
上記にもある通り,重み付け加重和の手法では以下に記す重大な欠点がある.
- 重みの分布を均等にしても,パレートフロント上の点は均等に分布しない.
- パレートフロントの非凸領域を検出することが不可能である.幾何学的に,そのような領域に対応する点を生成する重みの組み合わせを見つけることはできない([8]).
重み付によってパレートの情報が失われてしまっている.
正規境界交差法(Normal Boundary Intersection, NBI)
知っておこう.
- ユートピア点(utopia point) J^:各目的関数の個別最小値 J^_i を要素とするベクトルである.これは,目的が互いに競合している場合には達成不可能な点である([9]).
- 個別最小値の凸包(CHIM: Convex Hull of Individual Minima):目的空間における各目的の個別最小点を結んでできる超平面である.
step1: ユートピア点を求める
各目的の最適化度合いが MAX の点を考える.例えば,最速で精度 100%.
これを原点とする.(最小化問題の仮定)
step2: 一目的特化の点を考える.
精度 MAX の点,速度 MAX の点を考える.
通常この点は軸と重なる場合が多い.
step3: 一目的特化の点を結び,それと垂直な線を複数考える.
step4: ユートピア点に向かう最適化を行い,一番遠い実行可能解がパレートフロントを成す点である.
\[\min_{y} \max_{i=1,2,...,m} \left\{ \frac{J_i(y) - z_i}{s_i} \right\}\]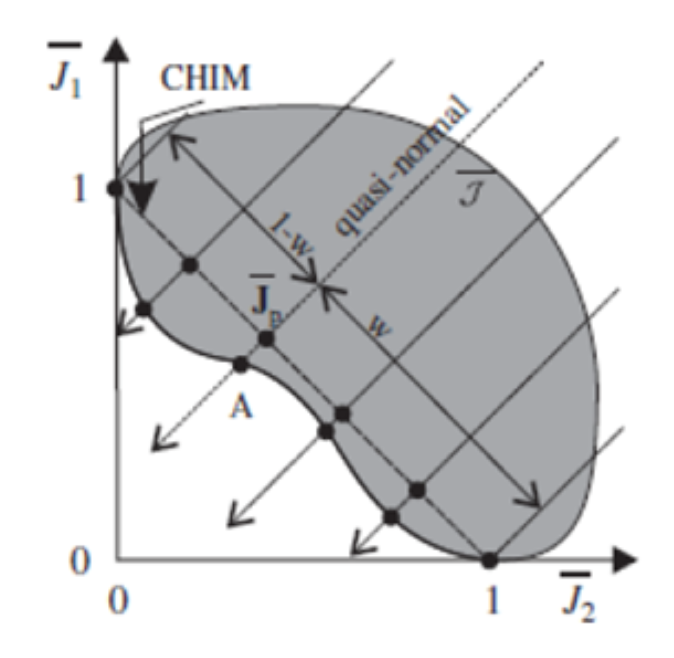
NBI の BAD POINT
- パレートフロントの解像度をトレードオフの内容に応じて変化させることができない.つまり,トレードオフが小さい領域でも,大きい領域と同じ密度で点が生成される.
- 実行の結果として,パレート最適でない点(非支配でない点)が生成される場合がある.このため,後処理としてパレートフィルターを適用して除外する必要がある.
- この戦略には 2 目的以上(特に 3 目的以上)の問題で,パレート点が均等に分布しないという欠点があった.
(拡張)正規正規制約法((Enhanced) Normalized Normal Constraint, (E)NNC)
step1: ユートピア点を求める
step2: 一目的特化の点を求める.
step3: 一つの目的関数を最小化対象とし,他の目的関数をすべて「不等式制約」として扱うことで,実行可能な目的空間を制限する.
Posterior Pareto front analysis(後処理によるパレートフロントの分析)
得られた解のうち,他の点に支配されるものをすべて除去する. その結果,パレート最適解のみを含む集合が得られる
スマートフィルターは,グローバルパレート点の集合に対してペアごとの比較を行う. その目的は,「実用的に価値のない」点を除外することであり,具体的には,ある点が他の点のPIT 領域(Practically Insignificant Trade-off Region)に含まれるかどうかを調べることである.
PIT 領域は,2 つのパラメータ $\Delta_t$ および $\Delta_r$ によって定義される:
- $\Delta_t$:意思決定者が「有意なトレードオフ」と見なす最小の差異値を表す.
- 対応する目的関数の差が $\Delta_t$ より大きければ,有意なトレードオフとされる.
- よって,$\Delta_t$ が小さいほど,より高解像度のパレート表現が得られる.
- $\Delta_r$(任意):平坦な領域における点の密度を制御するために用いられる.
- 任意の 2 点の対応する目的関数の差が $\Delta_r$ を超える必要がある.
- $\Delta_r$ を大きくすると,平坦な領域での点の間隔が広くなる.
Solution of dynamic optimization problems
(動的最適化問題の解法)
(いったん略)
問題設定
\[\min_y \{ J_1(y), J_2(y) \}, \quad \text{s.t. } y \in S\] \[PF = \left\{ J(y) = (J_1(y), J_2(y)) \mid y \in S, \nexists y{\prime} \in S: J(y{\prime}) \prec J(y) \right\}\]目的
単に等間隔の点を並べるのではなく,
- トレードオフの激しい領域(knee や急峻な部分)には点を多く配置し,平坦な領域には少なくする
- パレートフロントの解像度をトレードオフの内容に応じて変化させる
解の質の高さに関する定義
Trade-off measure(トレードオフの測度)
\[T_d = \frac{ΔJ_1 - ΔJ_2}{\sqrt{(ΔJ_1)^2 + (ΔJ_2)^2}}\]- T_d = 1 のとき:第 1 目的関数が悪化し,第 2 目的関数が改善する方向
- T_d = -1 のとき:第 2 目的関数が悪化し,第 1 目的関数が改善する方向
- T_d = 0 のとき:両目的関数が等しく変化し,トレードオフがバランスしている
提案手法
提案アルゴリズム
2 つのパレート点間におけるトレードオフ度合いがあるしきい値 $\delta$ より大きい場合に限り,その中間に新しいパレート点の探索を行う.
1. 2つのパレート点 P_1,P_2 が与えられているとする.
2. それらの間のトレードオフ度合い T_d を計算する.
3. |T_d| > \delta であれば,新たな点 P_m をこの2点の間に追加し,再び P_1 と P_m,および P_m と P_2 のペアに対して同様のチェックを行う.
4. 逆に |T_d| =< \delta であれば,それ以上の点追加は不要と判断し,探索を打ち切る.
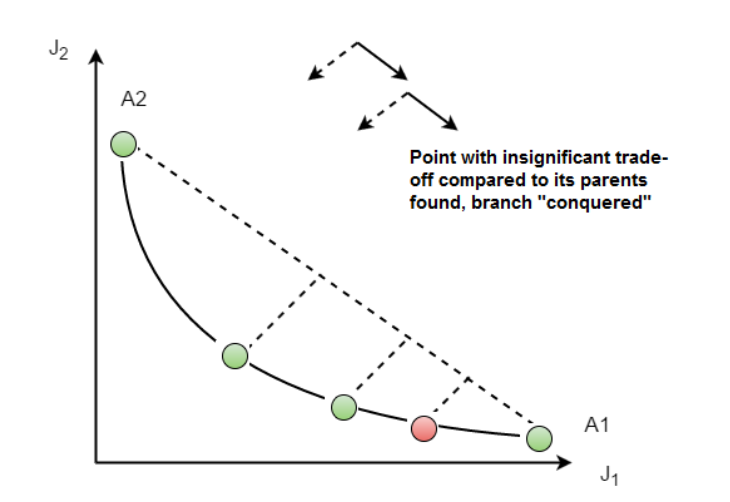
最小化問題であることに注意緑の点を見て,必要だと判断して赤の点を挿入する.
提案手法の GOOD POINT
- 事前にパレート点の総数を指定する必要がない
- トレードオフが顕著な部分のみに計算リソースを集中できる
- スマートフィルターと異なり,無意味な点を計算してから除外するのではなく,そもそも生成しない
結果
応用例として,フェドバッチバイオリアクターの最適化に適用し,その有効性を確認した.
なんじゃそれ
将来課題
高次元問題(3 目的以上)への拡張や,意思決定支援との統合が検討される.
参考文献
| 引用番号 | 著者名・出版年 | 論文タイトル | キーワード |
|---|---|---|---|
| [8] | Das, I. & Dennis, J. E. (1997) | A closer look at drawbacks of minimizing weighted sums of objectives for Pareto set generation | weighted sum の欠点,非凸フロント |
| [10] | Logist, F. et al. (2009) | Multi-objective optimal control of chemical processes using the normal constraint method | 動的最適化,化学プロセス,NNC 適用例 |
| [13] | Coello Coello, C. A. (1999) | A comprehensive survey of evolutionary-based multiobjective optimization techniques | vectorization,進化的アルゴリズム |
| [18] | Logist, F. et al. (2010) | Efficient handling of complex process models in multiobjective optimal control | scalarization 手法の概要,動的問題の定式化 |
| [19] | Das, I. & Dennis, J. E. (1998) | Normal-Boundary Intersection: A new method for generating the Pareto surface in nonlinear multicriteria optimization problems | NBI 提案論文 |
| [21] | Marler, R. T. & Arora, J. S. (2004) | Survey of multi-objective optimization methods for engineering | 多目的最適化手法のレビュー,分類 |
| [22] | Antipova, E. et al. (2015) | On the use of filters to facilitate the post-optimal analysis of the Pareto solutions | smart filter の提案と分析 |
| [23] | Logist, F. et al. (2012) | A posteriori multi-objective analysis of dynamic process optimization problems | 非パレート点除外,フィルターの必要性 |
| [24] | Miettinen, K. (1999) | Nonlinear Multiobjective Optimization | scalarization 理論の基本書 |
| [25] | Vallerio, M. et al. (2014) | An improved normalized normal constraint method for dynamic process optimization | ENNC の応用,化学プロセス |
| [26] | Vallerio, M. et al. (2015) | A tailored method for three-objective optimal control problems: the enhanced NNC method | ENNC 拡張,3 目的対応の正規化法 |
| [28] | Logist, F. et al. (2011) | Efficient deterministic implementation of reference point based multi-objective optimization strategies | deterministic MOO 手法実装 |