Multi-Objective Workflow Scheduling With Deep-Q-Network-Based Multi-Agent Reinforcement Learning
マルチエージェント強化学習でスケジューリング
概要
本研究では、クラウド環境におけるワークフロー処理の実行時間最小化とコスト最小化という 2 つの目的関数の最適化問題に対する手法を提案する。従来手法においては、専門家の知識に基づく静的な設計が必要とされていたが、本研究では各目的関数に対応する 2 つの Deep Q-Network (DQN)エージェントを用いたマルチエージェント強化学習(Multi-Agent Reinforcement Learning: MARL)アプローチを採用する。
提案手法では、各エージェントが他エージェントの行動を観測しながら、システム全体の報酬を最大化する戦略を相関均衡の概念に基づいて学習する。実験的評価により、提案手法は従来手法と比較して実行時間を大幅に短縮しつつ、同等のコスト水準を維持できることが示された。
背景
本研究は、クラウドコンピューティング環境におけるワークフロースケジューリング問題に対して、強化学習を用いた最適化手法を提案するものである。
ワークフローとは
- 複数の依存関係を持つタスクの集合
- DAG(有向非巡回グラフ)として表現される
問題設定
- タスクをどの VM に割り当てるかというスケジューリング問題
最適化指標
- 実行時間の最小化 VS コストの最小化
アプローチ
- メタヒューリスティック
- ゲーム理論ベースの手法
- Q 学習などの強化学習
本研究:DeepQNetwork によるマルチエージェント強化学習(MARL)
用語の整理
| 用語 | 意味 |
|---|---|
| ナッシュ均衡 | 各プレイヤーが他人の行動を固定と仮定して最適戦略を選ぶ状態 |
| 相関均衡 | 各プレイヤーが共同分布から得たシグナルに従うことで、誰も逸脱しない状態 |
| Q 値 $Q_i(s, a)$ | エージェント $i$ にとって、状態 $s$ で行動 $a$ を取るときの報酬期待値 |
| $\pi_s(a)$ | 状態 $s$ における行動 $a$ の共同分布(確率) |
| ワークフロー | 複数の依存関係を持つタスクの集合 |
| DAG(有向非巡回グラフ) | 有向非巡回グラフ |
関連研究や位置付け
既存の多くの手法は、「静的な視点」(全体があらかじめ分かっている前提)でスケジューリングを行う。
- 実際のクラウド環境は動的かつ不確実であり、これではうまく適応できない。
- 進化的アルゴリズムではエンコーディング設計や初期パラメータが専門家に依存する。
- 交差率,突然変異率など
機械学習でも学習率とかは専門家依存だけどなぁ
強化学習の他より良いところは?
- 逐次的に方針を更新できる.
- 状態空間と報酬だけ定義すれば自動的に学習できる
- 複数目的に対しても柔軟
その報酬の設計の難しさについて議論しないのはまずい気もする.
| 略語・手法 | 説明 |
|---|---|
| MOBFOA | Multi-objective Bacteria Foraging Optimization Algorithm:細菌行動に基づく進化的最適化 |
| BOGA | Bi-objective Genetic Algorithm:2 目的遺伝的アルゴリズム |
| GA-ETI | Genetic Algorithm with Efficient Tune-In:GA の性能を改善した手法 |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II:非支配ソートに基づく進化戦略 |
| MOPSO | Multi-objective Particle Swarm Optimization:粒子群最適化の多目的版 |
| GTBGA | Game-Theoretic Based Greedy Algorithm:ゲーム理論に基づく貪欲法 |
| RL | Reinforcement Learning(強化学習) |
| MARL | Multi-Agent Reinforcement Learning(マルチエージェント強化学習) |
DQN-MARL アルゴリズム
↓ をエージェントがそれぞれ行う.
-
初期化フェーズ
- 経験再生メモリ $D$ を初期化
- Q 関数(DQN)をランダムな重み $\theta$ で初期化
- 状態 $s$ と行動プロファイル $a$ を初期化
- 初期状態 $S$ を観測
-
学習ループ ($\text{max_episode}$ まで繰り返し)
2.1 行動選択
- 確率 $\varepsilon$ でランダムな行動 $a$ を選択 (探索)
-
確率 $1-\varepsilon$ で選択メカニズム $f$ に従い行動 $a$ を選択 (活用)
2.2 環境とのインタラクション
- 選択した行動 $a$ を実行
- 報酬 $r$ と次状態 $s’$ を観測
-
経験 $\langle s, a, r, s’ \rangle$ をメモリ $D$ に保存
2.3 学習ステップ
- $D$ からミニバッチ $\langle ss, aa, rr, ss’ \rangle$ をサンプリング
- 各遷移に対しターゲット値を計算:
- 終端状態の場合: $tt = rr$
- それ以外: $tt = rr + \delta \max_{a’} Q(ss’, a’)$
-
損失 $(tt - Q(ss, aa))^2$ で Q-network を更新
2.4 状態更新
- $s \leftarrow s’$
-
出力
- Q 値
- 行動プロファイル
- 報酬
Q. トレードオフっていっぱい点あるし,極端な点も出てしまうのでは?
A. あまり弁明されていない.
In order to resolve this problem, we introduce an utilitarian selection mechanism [ f = \max{\pi_s \in \Delta(A(s))} \sum{j \in I} Q_j(s, a) ] which donates maximize the sum of all agents’ rewards in each state.
それぞれの Q 値の合計を最大にする方策を選択するので,片方が損なわれている解は選ばれにくい.という(遠回りな)主張
Although MOPSO algorithm is cheaper than our proposed algorithm, our proposed algorithm clearly beats baseline ones in terms of make-span, and our algorithm is much cheaper than the GTBGA and only 2.899%, 4.303% more expensive than NSGA-II and MOPSO, respectively when task size is 138.
片方を大きくしつつ,片方の損失は最小化されている.
そもそも報酬設計が,小さな改善の価値を強調し,大きな悪化を抑制する非線形性を持っている. 自然と両者のバランスがとられるのだ.
報酬設計
| エージェント | 報酬関数 | 説明 |
|---|---|---|
| Make-span (R1) | $\left[\frac{ET_{k,i,j}(a) - (makespan’ - makespan)}{ET_{k,i,j}(a)}\right]^3$ | 現在のタスク割当による make-span の変化(改善なら報酬大) |
| Cost (R2) | $\left[\frac{worst - ET_{k,i,j}(a) \cdot p(j)}{worst - best}\right]^3$ | 実行コストが最悪ケースに比べてどれだけ小さいか(低いほど報酬大) |
実験
CyberShake などのベンチマーク. Amazon EC2 で動作させる.
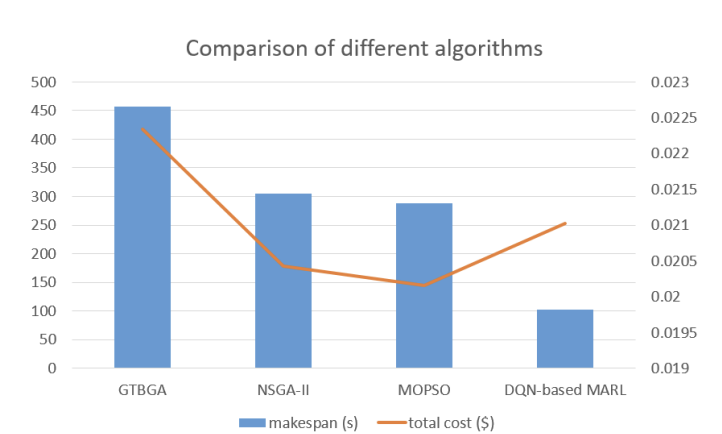
- NSGA-II と比較しても 2.899%,MOPSO に対しては 4.303%の追加コストである.
- タスク数が 138 のときの結果でこれを示しており,コスト面でも十分に競争力がある.
コスト上がっている. コストの上昇幅に対して待ち時間がかなり減っているとの主張があるが,パレートの議論をせずにこの主張をするのは無理があるのでは 4%が十分小さいというのが共通理解であれば問題ないかもしれない.
スケジュールの図かパレート解集合のどちらかは必要そうだと感じた.